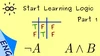
- 1
- 12
I was studying linear algebra and was reminded of this book that I bought some time ago. I haven't finished it (2 chapters in) but the introductory concepts coupled with my random study of SU(2) group and its algebra gave me some rudimentary insight into the utility of Lie Algebra's and why it was good enough to be used for Pauli matrices and describing spin, but not good enough to be true vectors in 3-d+1 time space.
For those interested, there is also a good channel that goes over the boom in-depth and you can pretend youre a graduate student getting lectures and working problems from the book as homework.
Here is thw link
- 3
- 11
Most of the nobel prizes are b.s. political trash, but science is less affected with the trash of humanity. The physics winners goes to the three people that shown that bell's inequality can be broken with a specific experimental set-up, the person who did the experiment, and the person who applied it to create quantum computing. If microscopic engineering improves and current atom by atom materials construction techniques can be industrialized we may see a phase of technology where the spin parity of photons instead of electrons can be used for quantum computing. Of course reality limits technology, but innovation uses limitations to create technology!
- 1
- 12
Bought this book after seeing it referenced in Jackson's "Classical Electrodynamics" and so far it is wonderful. I have only grazed the surface, but just from the concise and explicit definitions given it seems wondeful. However, there is only slight intersections with Electrodynamics since the topic covers optics rather than the general topic of electromagnetic phenomena.
The book is called "Principles of Optics" by Born and Wolf.
- 1
- 10
Seriously though, go through your book aswell bud.
- 4
- 11
Im not going to do them cause I've already done them. But here ya go! Taken from "Introduction to Real Analysis," by William Trench
- 2
- 11
I enjoyed them. The first book is good on its own, supplemental resources arent really needed and the main citations are from direct translations. The second book is really big and long amd goes in depth on newton's "principia naturalis..." Researching the cited sources in conjuction to the text is actually extremely useful. Especially, for those not acquainted with the old school of thought in mathematics and the pedagogical rigor that it contains.
- WEAL_KEV_TV_REBORN: fake rocket lover
- 2
- 10
I like this guys channel. He does nice softcore examples of proofing techniqies generally required and even does and a set theory basis for the natural numbers rather than the usual peano's axioms.
- 1
- 10
I just found out recently that converting between number systems (i.e. decimal to binary) uses successive multiplications or divisions depending on the digit placement. Then it dawned upon me, so is this why logarithms and modulizing number systems are interesting in Number theory. I always wondered why they make computer engineers study number theory.
Its a pretty interesting topic to dive into.
I dont have any links really have links on this one. Mayber check out the history of logarithms and see the correlation.
I would look at the translated version of "Mirifici Logarithmorum Canonis Descriptio," and look at what mods do.
For instance, using the integer number system and modulizing it by 2, I build the set of number which could be represented as binary numbers.
- 2
- 10











](/images/16613743797200134.webp)